Сетевой график в бизнес плане
Сетевой график – это динамическая модель проекта, которая отражает последовательность и зависимость работ, необходимых для успешного завершения проекта. Сетевой график отражает сроки выполнения запланированных работ и ресурсы, необходимые для их выполнения, а также прямые финансовые затраты, возникающие при реализации этих работ.
В английском языке для определения сетевого графика используется термин Project Network — is a graph depicting the sequence in which a project’s terminal elements are to be completed by showing terminal elements and their dependencies.
Основной целью использования сетевого графика является эффективное планирование и управление работами и ресурсами проекта. При этом, под ресурсами в данном контексте понимается как оборудование, производственные мощности или денежные средства, так и трудовые ресурсы, внутренние или внешние для организации, выполняющей проект.
Наибольшая эффективность применения сетевого графика достигается при его использовании для планирования проектов или отдельных взаимосвязанных работ. Сетевой график позволяет довольно точно определить плановые сроки завершения проекта и выявить возможные варианты их сокращения. И, что более важно, сетевой график позволяет на ранней стадии планирования проекта выявить критический путь. Кроме этого сетевой график позволяет осуществлять базовый контроль над ходом работ проекта, их сроками и исполнением бюджета.
Виды сетевых графиков
Сетевой график — это граф, на котором события (состояния работ или объектов в определенный момент времени) представлены в виде вершин, а работы проекта представлены в виде дуг, соединяющих вершины графа. Сетевой график, представленный в таком виде, изначально является частью метода PERT (Program Evaluation and Review Technique).
На практике же чаще используется другой вариант сетевого графика, когда вершинами графа являются работы, а дуги обозначают взаимосвязь между ними. Такой вид сетевого графика является частью метода критического пути (англ., CPM — Critical Path Method).
Рассмотрим второй вариант графика и алгоритм его построения подробнее.
Алгоритм построения сетевого графика
Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.
Шаг 1. Определить основную цель проекта
Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.
Шаг 2. Выявить ограничения
Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.
Шаг 3. Определить состав работ
Определить состав работ, необходимых для достижения цели, поставленной на шаге 1.
Шаг 4. Оценить длительность работ
Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.
Шаг 5. Определить последовательность работ
Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.
Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.
Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.
Шаг 6. Указать связи между работами
Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.
Шаг 7. Определить раннее начало и раннее окончание
Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.
Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.
Шаг 8. Определить поздние начало и окончание
Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
Шаг 9. Определить временной резерв
Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
Шаг 10. Выявить критический путь
Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.
Пример построения сетевого графика
Несмотря на то, что описанный выше алгоритм может показаться сложным, на самом же деле построение сетевого графика задача несложная. Для того, чтобы убедиться в этом рассмотрим построение сетевого графика на простом примере ремонта детской комнаты.
Шаг 1. Определить основную цель проекта
Представьте, что сейчас лето, вашему сыну исполнилось 7 лет и в сентябре он идет в школу. Вы решил обновить его комнату к новому учебному году и сделать ее подходящей для школьника, т.е. должно появиться полноценной рабочее место, зонирование комнаты измениться, и т.д.
В этом случае целью нашего небольшого проекта будет — сделать комнату пригодной и приятной для проживания мальчика, который пойдет в начальную школу.
Шаг 2. Выявить ограничения
Бюджет не более 100,000 руб., ремонтные работы можно вести только в рабочие дни с 10:00 до 18:00 с обязательным перерывом с 12:00 до 14:00. Итого получается — 6 рабочих часов в день.
Шаг 3. Определить состав работ
Немного поразмыслив мы накидали основные работы, которые надо сделать, а именно:
- Нам нужен дизайн-проект новой комнаты;
- Нам надо закупить материалы для ремонта;
- Надо составить смету ремонта;
- Надо выполнить сам ремонт;
- И т.к. мы решили сделать небольшую перепланировку, то надо согласовать ее с ТСЖ.
Отобразим эти работы в виде блоков:
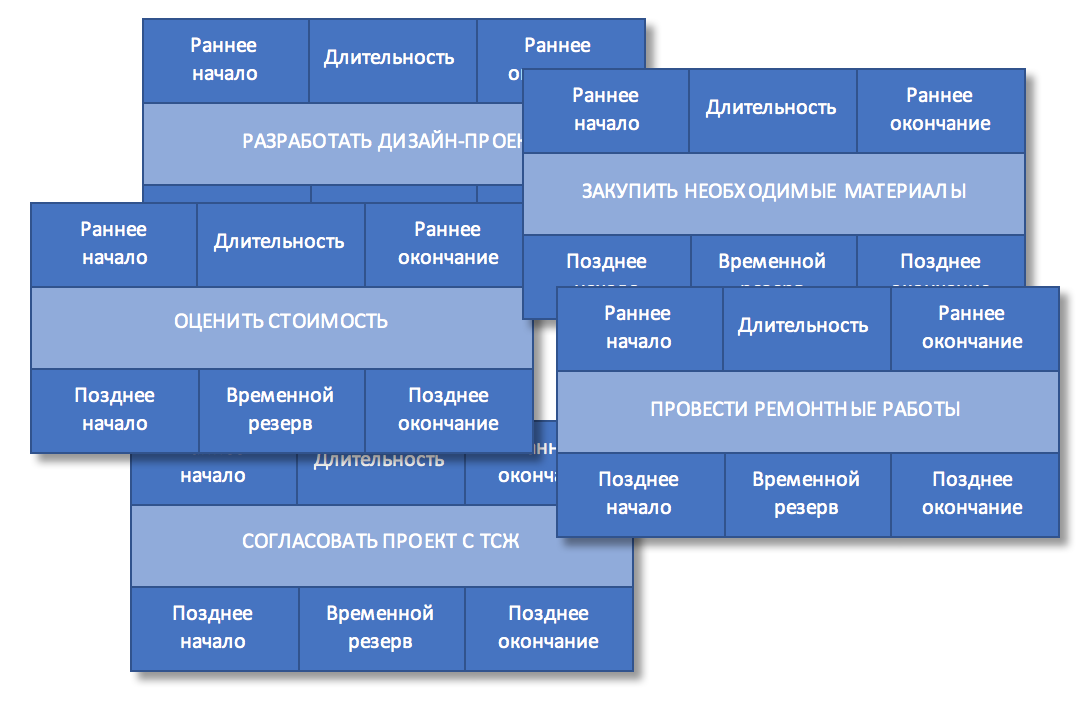
Рисунок 1. Состав работ
Шаг 4. Оценить длительность работ
Мы решили оценивать длительность работ в днях, т.к. до начала учебного года еще достаточно времени, то такая точность планирования нас вполне устраивает.

Рисунок 2. Длительность работ
Шаг 5. Определить последовательность работ
Теперь определим последовательность работ, мы будем использовать схему построения сетевого графика «сверху-вниз». Первая работа, которую необходимо выполнить — это работа «Разработать дизайн-проекта«. Затем мы оценим стоимость проекта, а параллельно начнем согласование с ТСЖ, т.к. эта задача занимает много времени. После того, как мы оценим проект и его согласуем, мы приступим к покупке всех необходимых материалов и уже затем начнем сам ремонт.

Рисунок 3. Последовательность работ
Шаг 6. Указать связи между работами
Укажем стрелками связи между работами.

Рисунок 4. Связи между работами
Шаг 7. Определить раннее начало и раннее окончание
Т.к. мы выбрали модель сетевого график «сверху-вниз», то начинаем его и просматривать сверху вниз, начиная с самой верхней работы, и далее по очереди двигаемся к самой нижней работе.
Напомним, что раннее начало последующей работы будет совпадать с ранним завершением предшествующей, а раннее окончание каждой из работ определяется как раннее начало плюс длительность работ Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ.
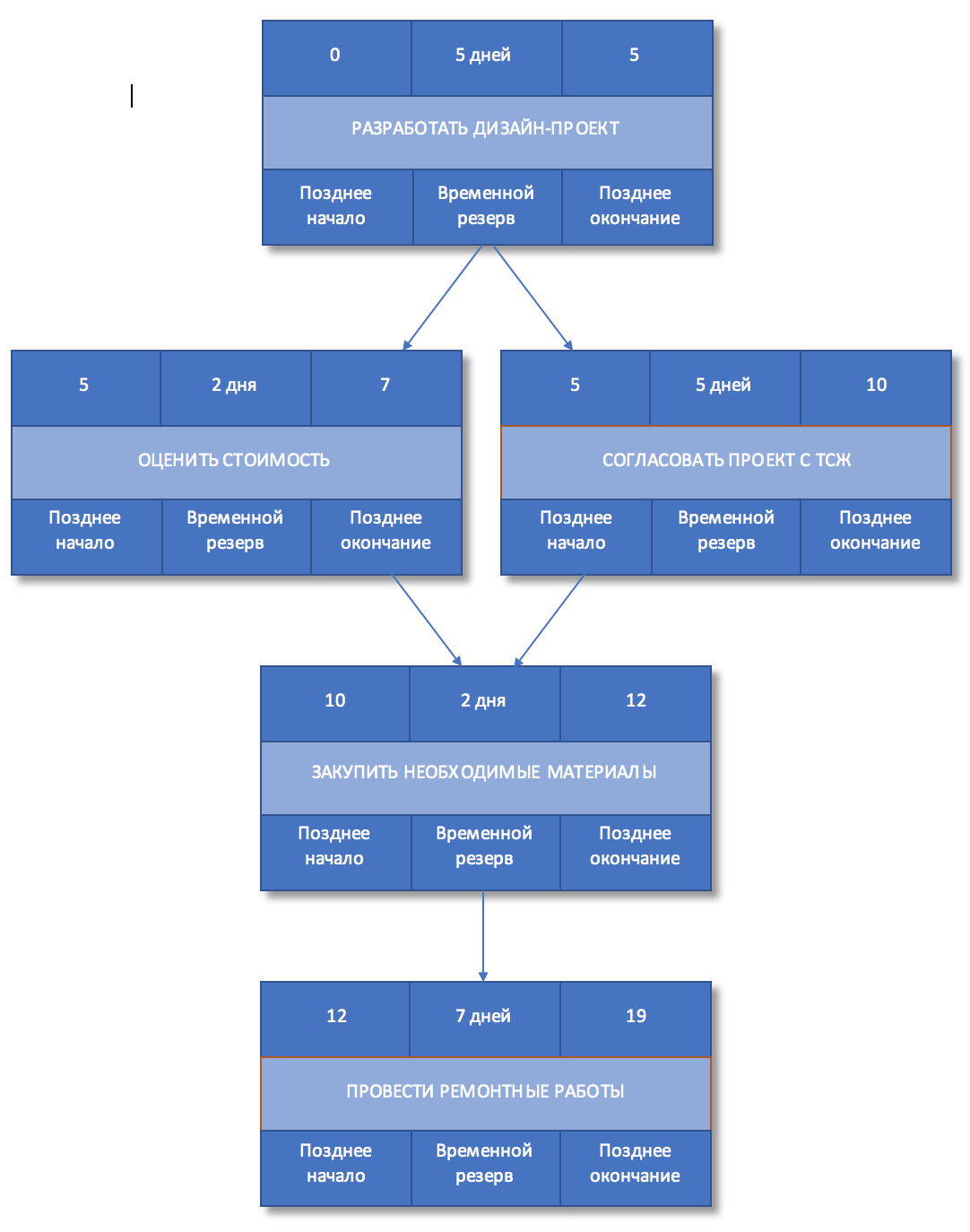
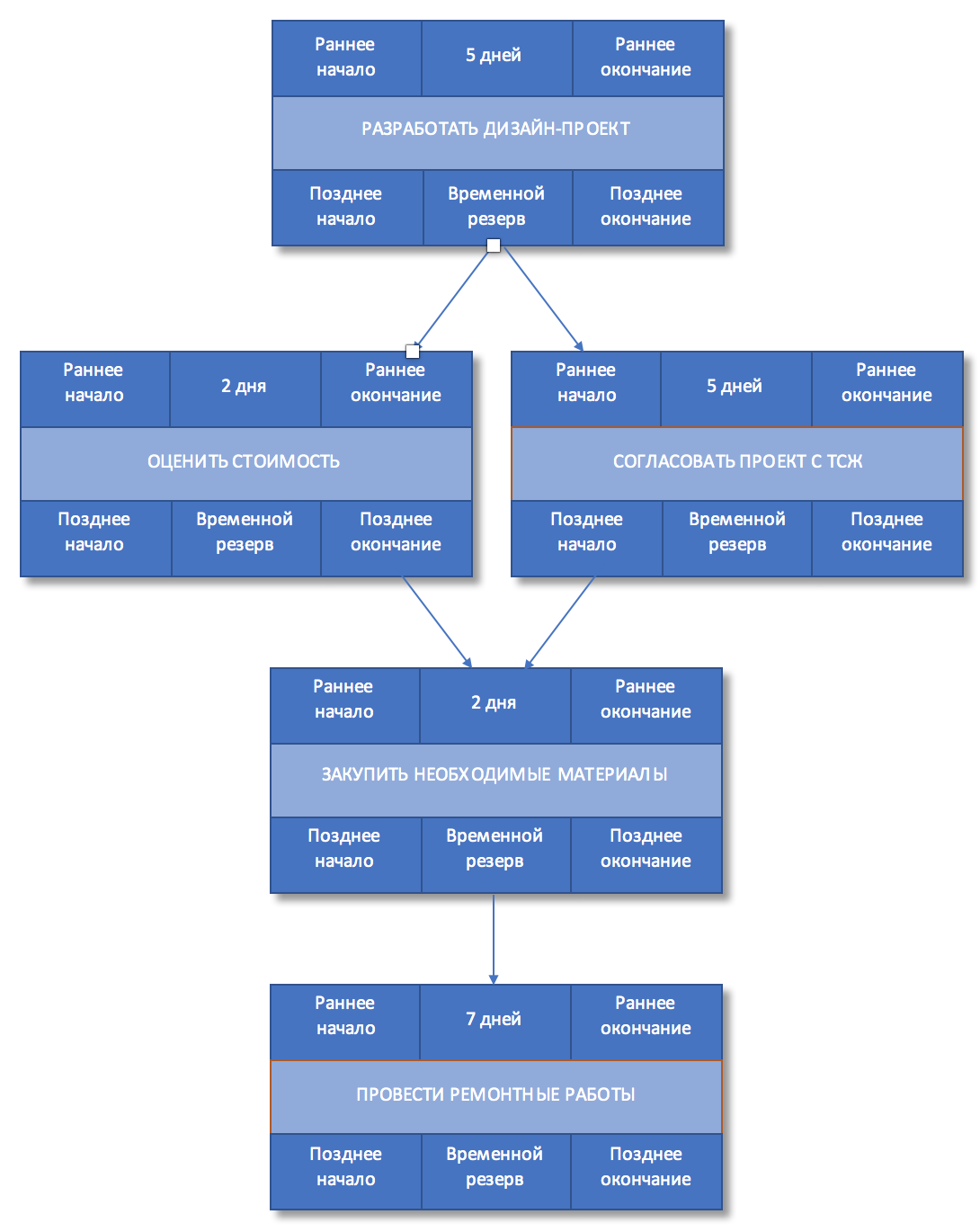
Рисунок 5. Раннее начало и окончание работ
Шаг 8. Определить поздние начало и окончание
Для того, чтобы определить поздние начало и окончание просмотрим сетевой график в обратном направлении — снизу вверх. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
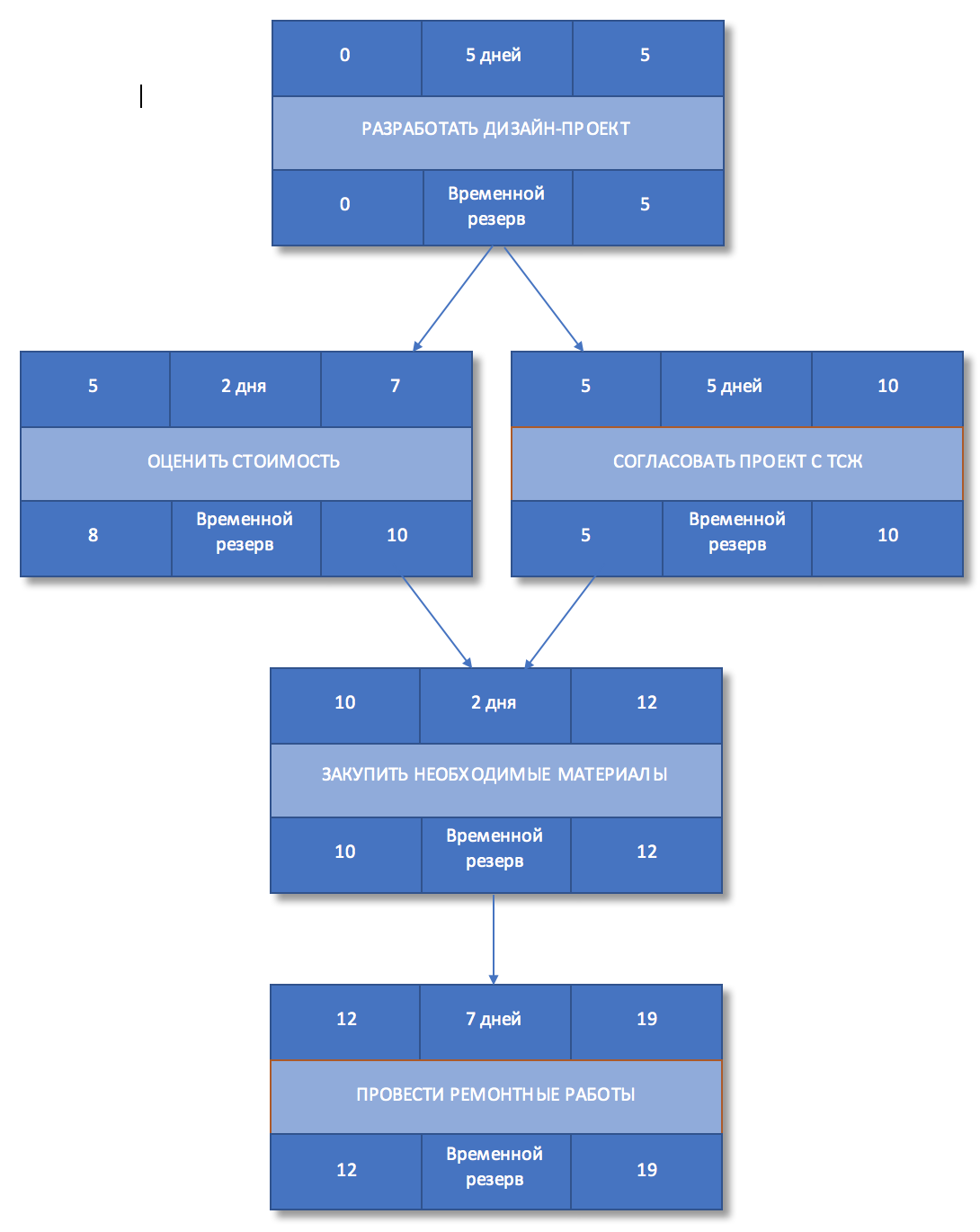
Рисунок 6. Позднее начало и окончание работ
Шаг 9. Определить временной резерв
Вычислим временной резерв для каждой из работ. Он вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
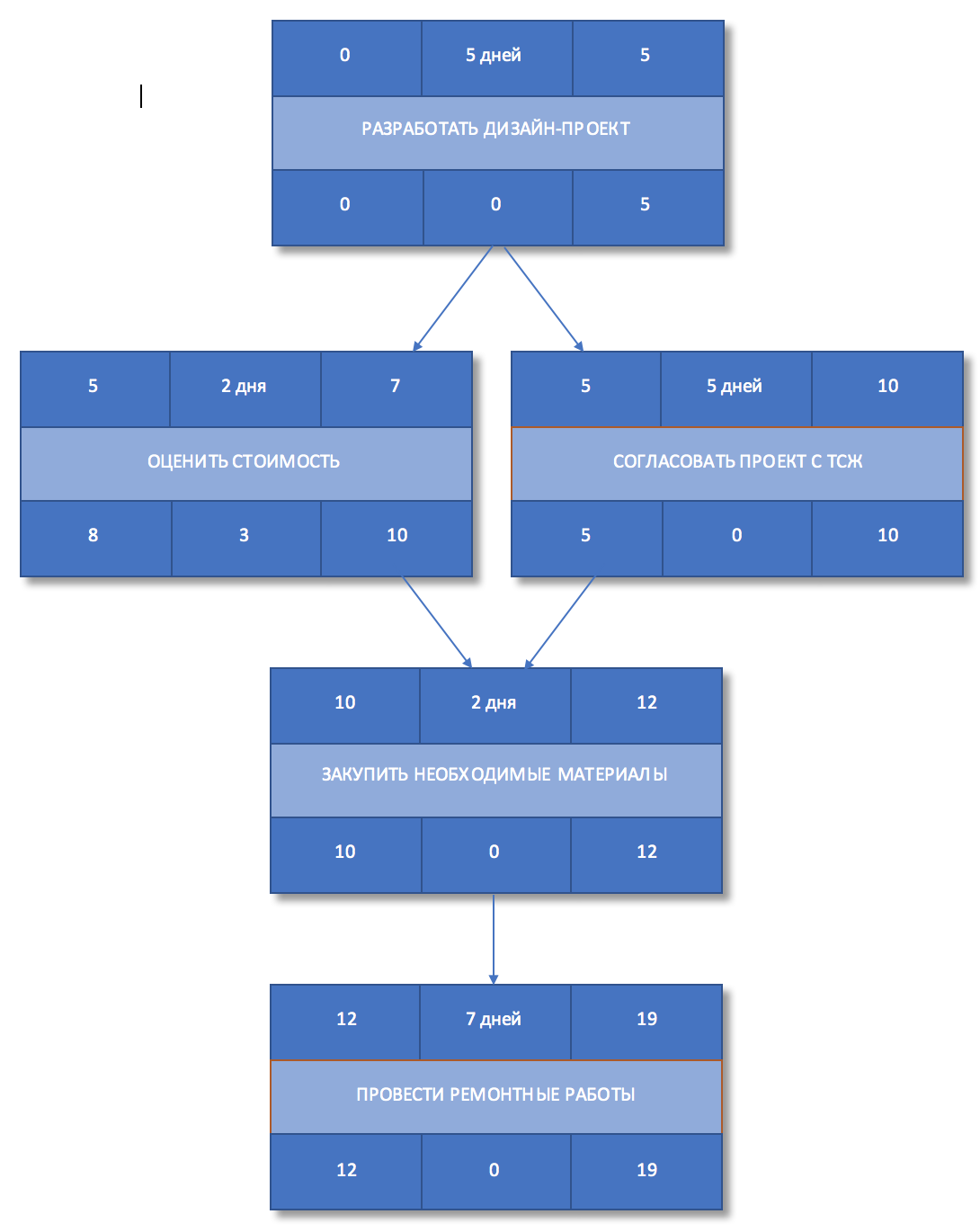
Рисунок 7. Временной резерв
Шаг 10. Выявить критический путь
Как мы уже знаем, критический путь — это цепочка работ, у которых резерв времени равен нулю. Выделим такие задачи на сетевом графике.
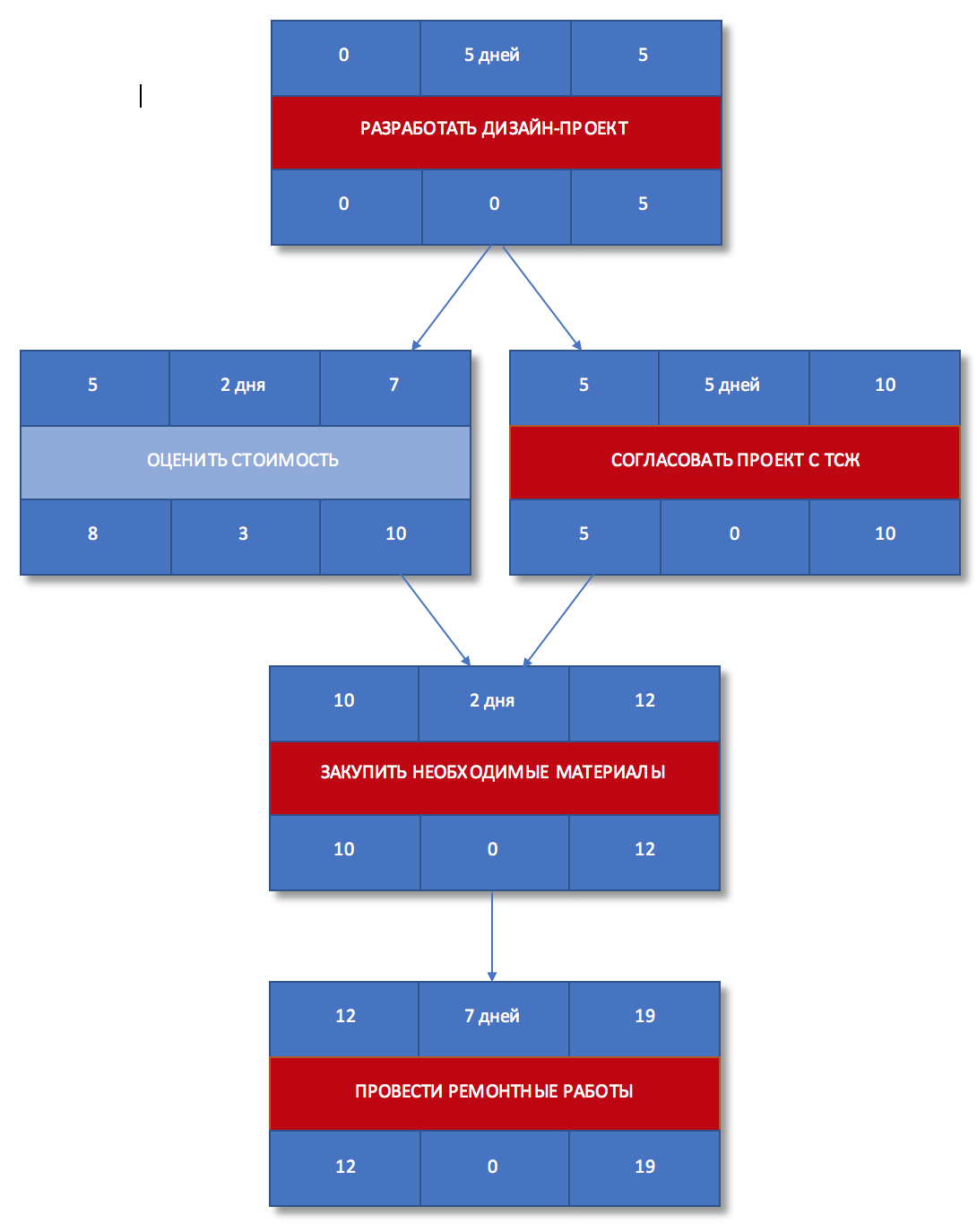
Рисунок 8. Критический путь
Задачи «Разработать дизайн-проект«, «Согласовать проект с ТСЖ» и «Закупить необходимые материалы«, «Провести ремонтные работы» составляю критический путь, а его длина составляет 19 дней. Это означает, что в текущем виде проект не может быть выполнен быстрее, чем за 19 дней. Если мы хотим сократить сроки проекта, то нам необходимо оптимизировать задачи, лежащие на критическом пути.
Например, мы можем начать ремонтные работы раньше получения согласования на перепланировку от ТСЖ, приняв на себя риски того, что согласование может быть не получено.
Просмотры:
59 949
Источник

Автор статьи:
Основатель Projectimo.ru
Свежие публикации автора:
Менеджер проекта, занимаясь его планированием, должен помнить о проектном треугольнике ограничений: «продолжительность» – «стоимость» – «содержание». Ресурсные и стоимостные ограничения предопределяют качество расписания проекта. Сетевое планирование, хотя и является достаточно рутинным инструментом календарной проработки, тем не менее, позволяет лучшим образом выполнить оптимизацию плана в отношении ресурсов и сроков. Сетевой график, построенный по методу «вершина – работа», предоставляет все возможности применения прикладных методов оптимизации.
Глоссарий разработки сетевого графика
Построение сетевого графика методологически основано на общей концепции СПУ (системы планирования и управления) проектов. Ключевые аспекты данной методологии были рассмотрены в статье на тему сетевого планирования проекта. В настоящем материале мы развиваем начатое осмысление теоретических и прикладных вопросов сетевого моделирования. В первую очередь, нас интересует разработка сетевой диаграммы вида «вершина – работа» в контексте ее составления, оптимизации и корректировки. Логика сетевого планирования достаточно проста, математически метод не сложен.
Тем не менее, на практике применить полноценно эту модель удается не всегда. Возникают затруднения, во многом определяемые психологией участников, не готовых объективно рассчитать сроки исполнения сформулированных задач. Данный метод дает более слабый результат в условиях перегруженности ответственных ресурсов по проектным задачам. Сетевые графики хорошо работают в проектах, где ответственные исполнители заняты только на одном проекте, например, в строительстве. Ниже показана модель процесса календарного планирования, которая служит направляющим ориентиром в работе со средством планирования «сетевой график».

Схема разработки календарного плана проекта
Введем основные понятия, которые понадобятся для составления сетевой модели проекта и ее оптимизации:
- отношение предшествования – это характеристика связи последующей работы в отношении предшествующей;
- путь – это непрерывная последовательность операций (работ) в сетевом графике;
- предшествующий путь – участок полного пути от исходного до рассматриваемого события;
- последующий путь – участок полного пути от рассматриваемого события до любого следующего;
- критический путь – это полный путь, характеризуемый нулевым резервом;
- критическая работа – действие, для которого полный резерв имеет нулевое значение;
- предкритическая работа – операция, для которой менеджер проекта установил число предельного значения полного резерва;
- резерв пути – разница между временной длительностью проекта и длиной пути на графике;
- веха – работа с нулевой продолжительностью, обозначает важное, значимое событие в проекте;
- минимальное время от начала проекта до начала выполнения операции без нарушения отношения предшествования называется ранним сроком начала работы;
- максимальное время с начала проекта до начала выполнения операции, которое позволяет проекту закончиться вовремя без нарушения отношения предшествования, называется поздним сроком начала работы;
- минимальное время, которое требуется для выполнения всех работ без нарушения отношения предшествования, называется ранним окончанием проекта;
- возобновляемый ресурс предполагает ограничение в использовании его на каждом шаге планируемого периода;
- невозобновляемый ресурс предполагает ограничение в использовании его на всем периоде реализации проекта.
Базовый алгоритм и виды связей сетевого графика
Сетевой график позволяет увидеть структуру работ, представить все этапы и взаимосвязи с требуемой степенью детализации. На его основе производится разработка обоснованного плана мероприятий с учетом более эффективного использования ресурсов по заданным критериям. Диаграмма позволяет производить поливариантный анализ альтернативных решений для улучшения календарного плана с использованием компьютерных технологий. Вспомним основные правила построения сетевой модели метода «вершина – работа».
- Элементы сетевого графика включают работы и зависимости (связи) между ними. События на графике не отражаются за исключением вех, представляющих собой основные наиболее важные события, изображаемых в форме «ромбиков», работ с нулевой продолжительностью.
- Работа представляет собой неделимый элемент процесса, требующий времени и других ресурсов для выполнения, изображается в виде прямоугольника, вытянутого по горизонтали. Исходя из этого правила, длина прямоугольника может свидетельствовать о продолжительности операции.
- Разработка графика начинается с размещения на нем исходной работы в крайней левой точке и завершается включением в него конечной операции, закрывающей проект. Календарно начальный момент исходного действия обозначает старт проекта.
- Зависимости (связи) между работами оформляются стрелками, направленными слева направо под разными углами наклона. На основе данного правила связи между операциями определяются одной из форм отношений зависимости.
- Сетевой график имеет только одну работу, в которую входят зависимости, но не выходит ни одна, и одну работу, не имеющей ни одной входящей зависимости.
- Сетевой график не может иметь циклов, т.е. зависимости не должны связывать работы по кругу.

Вид сетевого графика метода «вершина – работа»
Сетевой график строится по следующему алгоритму составления.
- На диаграмме размещается начальная работа проекта, не имеющая предшественников.
- Расположение операции, непосредственно следующей за работой, связанной с ней отношением предшествования, на графике левее предыдущей. Отображение связи предшествования.
- Переход к пункту 2 до тех пор, пока не закончатся работы, имеющие предшественников.
Разработка сетевой диаграммы производится с учетом возможных связей между работами. Основные виды отношений предшествования используются в четырех вариантах связей и в двух дополнительных их разновидностях. Далее на схеме представлены варианты связи следующей по идентификационному номеру работы к предыдущей или, наоборот, последующей. Основные или базовые виды предшествования связаны с перестановками слов «начало» и «окончание»:
- «окончание – начало» (простой вид отношения предшествования);
- «окончание – окончание»;
- «начало – начало»;
- «начало – окончание».
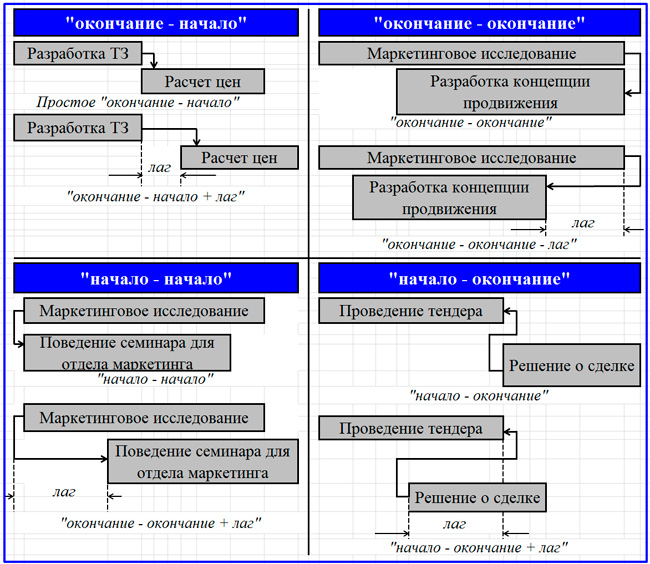
Примеры вариантов отношений предшествования
Методы расчета длительности операций
Для обеспечения построения, анализа и управления расписанием проекта необходимо рассчитать следующие параметры сетевого графика: стоимость, задействованные ресурсы и продолжительность работ. Требуемые ресурсы нужно рассчитать до определения продолжительности операций, так как их длительность во времени, как правило, зависит от состава задействованного ресурсного обеспечения. Кроме того, важно понимать, насколько ресурсы календарно доступны, что, в свою очередь, влияет на сроки работ и их продолжительность. Очевидно, что ключевым параметром выступает именно длительность операций. Для ее оценки используется ряд специальных методов, краткая характеристика которых приведена в табличной форме далее.

Основные методы оценки длительности операций
В случае отсутствия статистических данных по аналогичным операциям и невозможности применить экономико-математические методы расчета часто используют экспертные оценки. У данного метода есть серьезное достоинство – его простота, при условии, что удалось привлечь опытных и объективных экспертов. Но этого достичь бывает нелегко, позиции экспертов по вопросам продолжительности могут оказаться противоположными. Тем не менее, такое положение вещей вполне допустимо при использовании средневзвешенных оценок квалифицированных экспертных мнений.
В разнообразных проектах присутствуют идентичные по природе работы. Например, подготовка устава проекта, разработка ТЗ, проведение тендера по структуре и трудоемкости мало чем отличаются друг от друга. Это свойство используется для оценки длительности по аналогам. В некоторых случаях информацию о параметрах аналогичных работ вполне допустимо использовать для планирования расписания. Для этого схожесть типа и содержания операций должны быть подвергнуты экспертизе.
Параметрическая оценка длительности тесно сопряжена с нормативным подходом. Данный подход задействует такие параметры, в частности, как производительность (объем производства в единицу времени) или выработка. Например, чтобы выполнить монтаж I-го уровня сложности оборудования «А» требуется, допустим, 100 нормо-часов труда специалистов высшей квалификационной категории. Подобного рода мероприятия называют еще работами фиксированного объема, потому что продолжительность их связана с числом выделяемых ресурсов и может быть оценена как объем работ, деленный на количество человеческих ресурсов.
Помимо варианта фиксированного объема отдельно выделяется случай фиксированной продолжительности работы. Примерами таких работ являются действия, связанные с режимом дежурства на объекте, обслуживания оборудования и т.д. Продолжительность в подобных случаях обусловлена длительностью работы обслуживаемого объекта. Для параметрического метода, как мы видим, важно найти параметр, от которого зависит продолжительность операции и причинно-следственные связи, на основе которых возможно определить зависимости параметра от других значений.
Методы оптимизации сетевого графика
Сетевой график проектной реализации связан с содержанием уникальной задачи, параметрами времени и пространства, в которых выполняется проект. Данной деятельности присущи все традиционные функции управления без исключения. С этой точки зрения процесс можно разделить на этапы, в которых весомую долю занимает планирование. Далее вашему вниманию представляется упрощенная блок-схема функциональных этапов управления проектом.
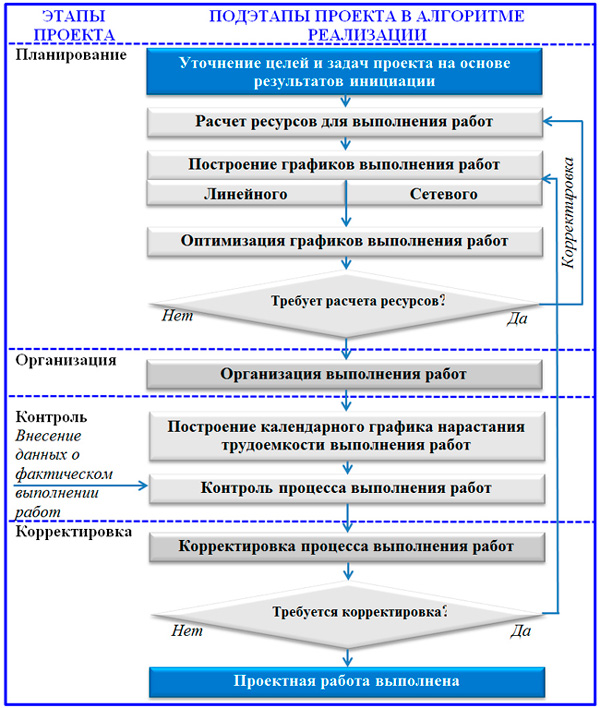
Функционально-процессная блок-схема управления проектом
На текущий момент нас интересует оптимизация сетевого графика как подэтап процесса планирования проектной задачи. Это связано с тем, что после сбора информации о работах и ограничениях разработка визуальной модели в форме сетевой диаграммы подразумевает дальнейшее ее улучшение с использованием методов расчета расписания. Основных методов два: метод критического пути (сокращенно МКП) и анализ расписания по методу PERT.
При использовании МКП производится последовательный расчет наиболее ранних и самых поздних сроков работ по проекту. Далее устанавливается размер полного резерва, при этом критическими работами считаются действия, имеющие нулевой полный резерв. Наконец, рассчитываются временные резервы для выполнения операций, и в качестве самого длинного пути сети выбирается критический путь. Критических путей может быть несколько. Оптимизация сетевого графика методом критического пути применяется для следующих моделей диаграммы:
- для моделей с дискретным и непрерывным временем;
- для моделей с простым отношением предшествования;
- в сетях с обобщенными связями.
Метод оценки и анализа программ (PERT) служит вторым методом, по которому проводится оптимизация сетевого графика. Его основные отличия от МКП основаны на допущении, что длительность работ носит случайный характер, и для целей оценки и анализа сроков следует учитывать неопределенность временного параметра работ проекта. Также делается допущение о независимости всех случайных величин продолжительности критического пути. Для этих целей на основе метода математической статистики и теории вероятности используется β-распределение и оценка параметров распределения с трех экспертных позиций: оптимистичной, пессимистичной и наиболее вероятной.
Корректировка сетевого графика и сокращение общей продолжительности проекта входят в состав ключевых задач проект-менеджера. МКП дает возможность рассчитать оптимальные сроки выполнения проекта, но не позволяет найти инструменты для более действенного сокращения его продолжительности. В этом отношении метод критического пути не обладает достаточной гибкостью. Метод PERT также не лишен недостатков. Во-первых, он нацеливает в основном на оптимистический вариант оценки, во-вторых, PERT в меньшей степени применим к небольшим проектным задачам.
Для эффективной корректировки лучше всего подходят такие современные методы, как метод критической цепи и методы сжатия. Им мы намерены уделить внимание в отдельной статье. Все названные модели и методы являются предметной зоной компетенций PM, владея которыми, менеджеру проще демонстрировать свою эффективность, достигая результата проекта в условиях временных и ресурсных ограничений.
Источник
