Сетевой график разработки бизнес плана
 Сетевой график – это динамическая модель проекта, которая отражает последовательность и зависимость работ, необходимых для успешного завершения проекта. Сетевой график отражает сроки выполнения запланированных работ и ресурсы, необходимые для их выполнения, а также прямые финансовые затраты, возникающие при реализации этих работ.
Сетевой график – это динамическая модель проекта, которая отражает последовательность и зависимость работ, необходимых для успешного завершения проекта. Сетевой график отражает сроки выполнения запланированных работ и ресурсы, необходимые для их выполнения, а также прямые финансовые затраты, возникающие при реализации этих работ.
В английском языке для определения сетевого графика используется термин Project Network — is a graph depicting the sequence in which a project’s terminal elements are to be completed by showing terminal elements and their dependencies.
Основной целью использования сетевого графика является эффективное планирование и управление работами и ресурсами проекта. При этом, под ресурсами в данном контексте понимается как оборудование, производственные мощности или денежные средства, так и трудовые ресурсы, внутренние или внешние для организации, выполняющей проект.
Наибольшая эффективность применения сетевого графика достигается при его использовании для планирования проектов или отдельных взаимосвязанных работ. Сетевой график позволяет довольно точно определить плановые сроки завершения проекта и выявить возможные варианты их сокращения. И, что более важно, сетевой график позволяет на ранней стадии планирования проекта выявить критический путь. Кроме этого сетевой график позволяет осуществлять базовый контроль над ходом работ проекта, их сроками и исполнением бюджета.
Виды сетевых графиков
Сетевой график — это граф, на котором события (состояния работ или объектов в определенный момент времени) представлены в виде вершин, а работы проекта представлены в виде дуг, соединяющих вершины графа. Сетевой график, представленный в таком виде, изначально является частью метода PERT (Program Evaluation and Review Technique).
На практике же чаще используется другой вариант сетевого графика, когда вершинами графа являются работы, а дуги обозначают взаимосвязь между ними. Такой вид сетевого графика является частью метода критического пути (англ., CPM — Critical Path Method).
Рассмотрим второй вариант графика и алгоритм его построения подробнее.
Алгоритм построения сетевого графика
Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.
Шаг 1. Определить основную цель проекта
Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.
Шаг 2. Выявить ограничения
Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.
Шаг 3. Определить состав работ
Определить состав работ, необходимых для достижения цели, поставленной на шаге 1.
Шаг 4. Оценить длительность работ
Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.
Шаг 5. Определить последовательность работ
Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.
Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.
Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.
Шаг 6. Указать связи между работами
Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.
Шаг 7. Определить раннее начало и раннее окончание
Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.
Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.
Шаг 8. Определить поздние начало и окончание
Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
Шаг 9. Определить временной резерв
Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
Шаг 10. Выявить критический путь
Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.
Пример построения сетевого графика
Несмотря на то, что описанный выше алгоритм может показаться сложным, на самом же деле построение сетевого графика задача несложная. Для того, чтобы убедиться в этом рассмотрим построение сетевого графика на простом примере ремонта детской комнаты.
Шаг 1. Определить основную цель проекта
Представьте, что сейчас лето, вашему сыну исполнилось 7 лет и в сентябре он идет в школу. Вы решил обновить его комнату к новому учебному году и сделать ее подходящей для школьника, т.е. должно появиться полноценной рабочее место, зонирование комнаты измениться, и т.д.
В этом случае целью нашего небольшого проекта будет — сделать комнату пригодной и приятной для проживания мальчика, который пойдет в начальную школу.
Шаг 2. Выявить ограничения
Бюджет не более 100,000 руб., ремонтные работы можно вести только в рабочие дни с 10:00 до 18:00 с обязательным перерывом с 12:00 до 14:00. Итого получается — 6 рабочих часов в день.
Шаг 3. Определить состав работ
Немного поразмыслив мы накидали основные работы, которые надо сделать, а именно:
- Нам нужен дизайн-проект новой комнаты;
- Нам надо закупить материалы для ремонта;
- Надо составить смету ремонта;
- Надо выполнить сам ремонт;
- И т.к. мы решили сделать небольшую перепланировку, то надо согласовать ее с ТСЖ.
Отобразим эти работы в виде блоков:
Рисунок 1. Состав работ
Шаг 4. Оценить длительность работ
Мы решили оценивать длительность работ в днях, т.к. до начала учебного года еще достаточно времени, то такая точность планирования нас вполне устраивает.

Рисунок 2. Длительность работ
Шаг 5. Определить последовательность работ
Теперь определим последовательность работ, мы будем использовать схему построения сетевого графика «сверху-вниз». Первая работа, которую необходимо выполнить — это работа «Разработать дизайн-проекта«. Затем мы оценим стоимость проекта, а параллельно начнем согласование с ТСЖ, т.к. эта задача занимает много времени. После того, как мы оценим проект и его согласуем, мы приступим к покупке всех необходимых материалов и уже затем начнем сам ремонт.

Рисунок 3. Последовательность работ
Шаг 6. Указать связи между работами
Укажем стрелками связи между работами.
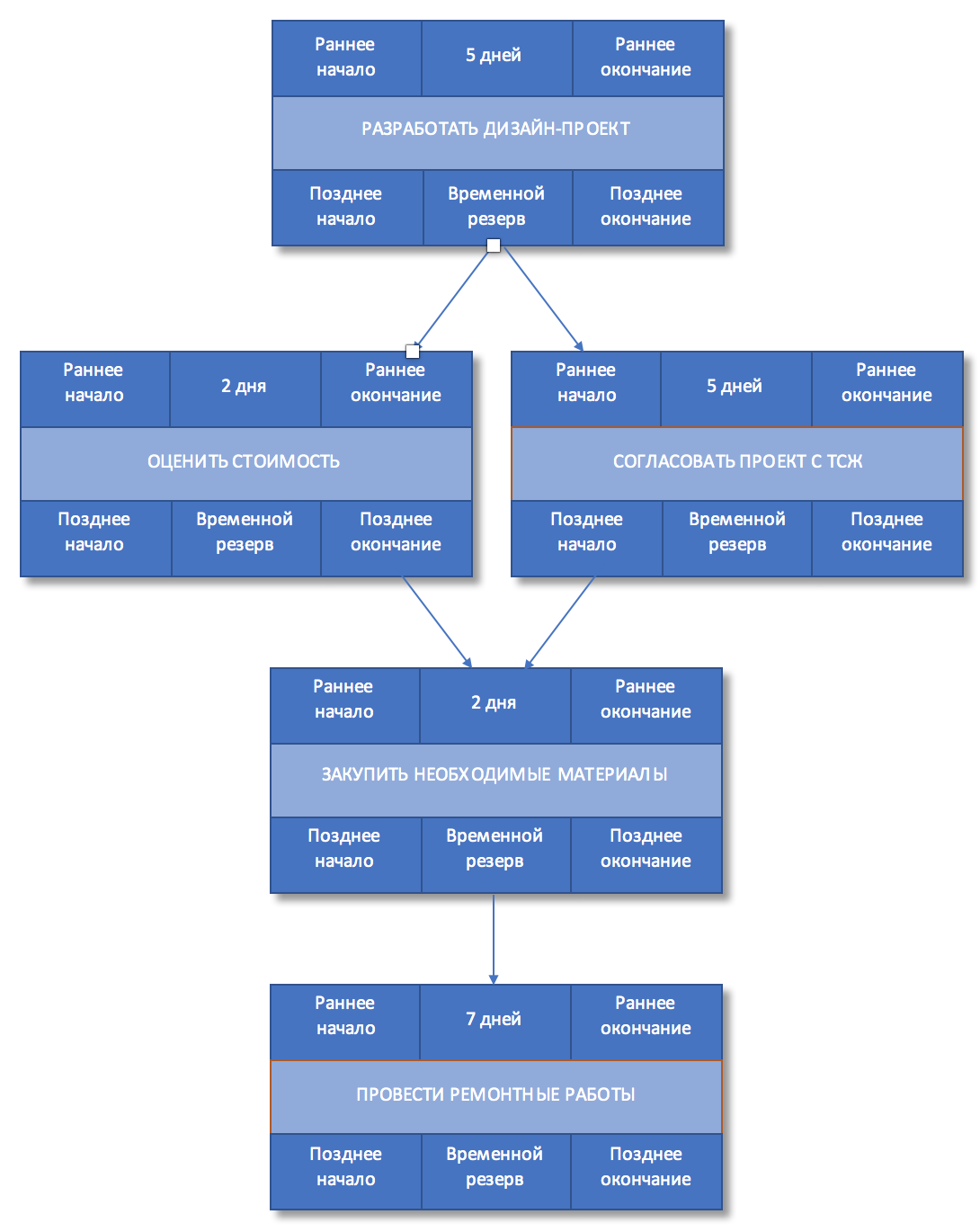
Рисунок 4. Связи между работами
Шаг 7. Определить раннее начало и раннее окончание
Т.к. мы выбрали модель сетевого график «сверху-вниз», то начинаем его и просматривать сверху вниз, начиная с самой верхней работы, и далее по очереди двигаемся к самой нижней работе.
Напомним, что раннее начало последующей работы будет совпадать с ранним завершением предшествующей, а раннее окончание каждой из работ определяется как раннее начало плюс длительность работ Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ.
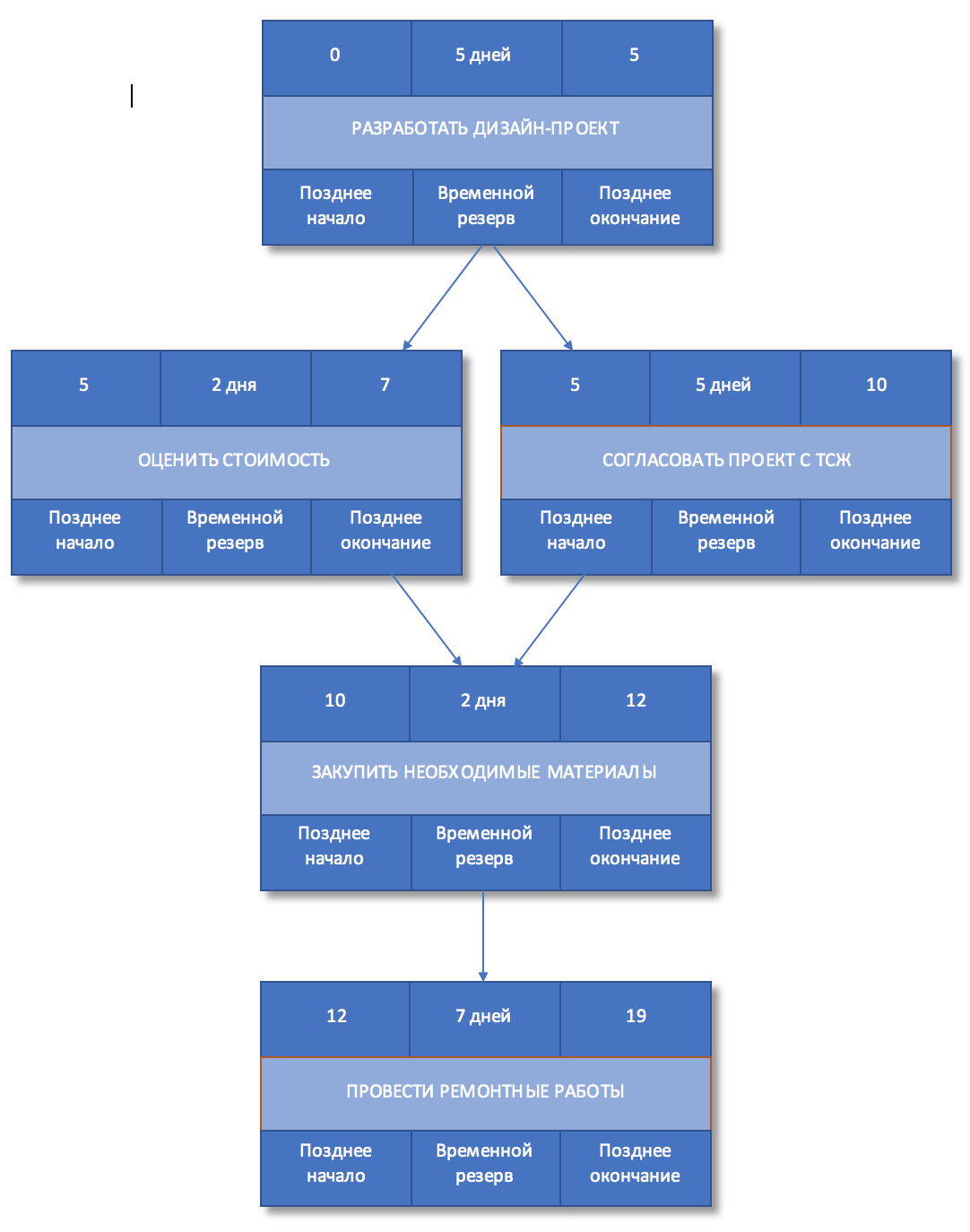
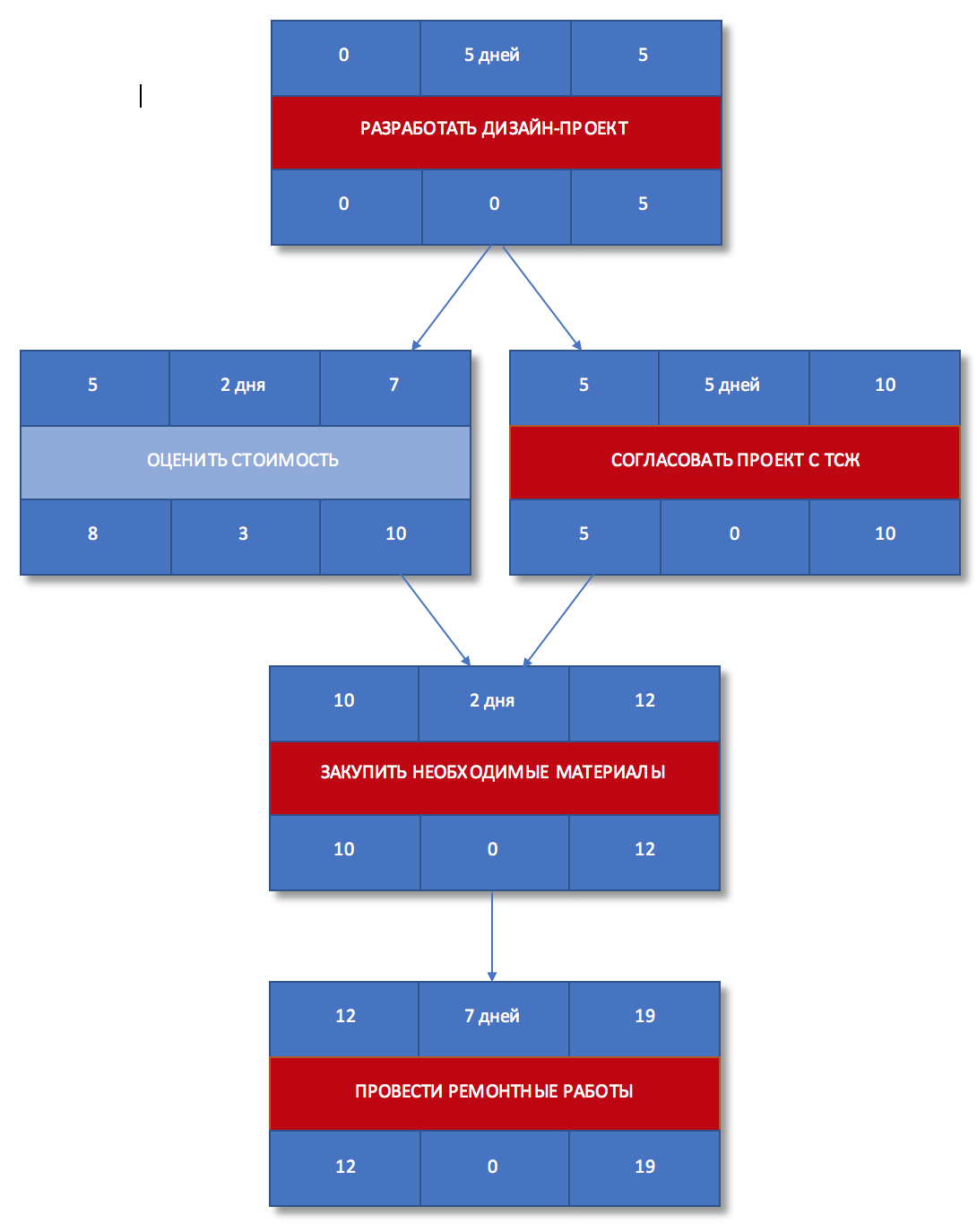
Рисунок 5. Раннее начало и окончание работ
Шаг 8. Определить поздние начало и окончание
Для того, чтобы определить поздние начало и окончание просмотрим сетевой график в обратном направлении — снизу вверх. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
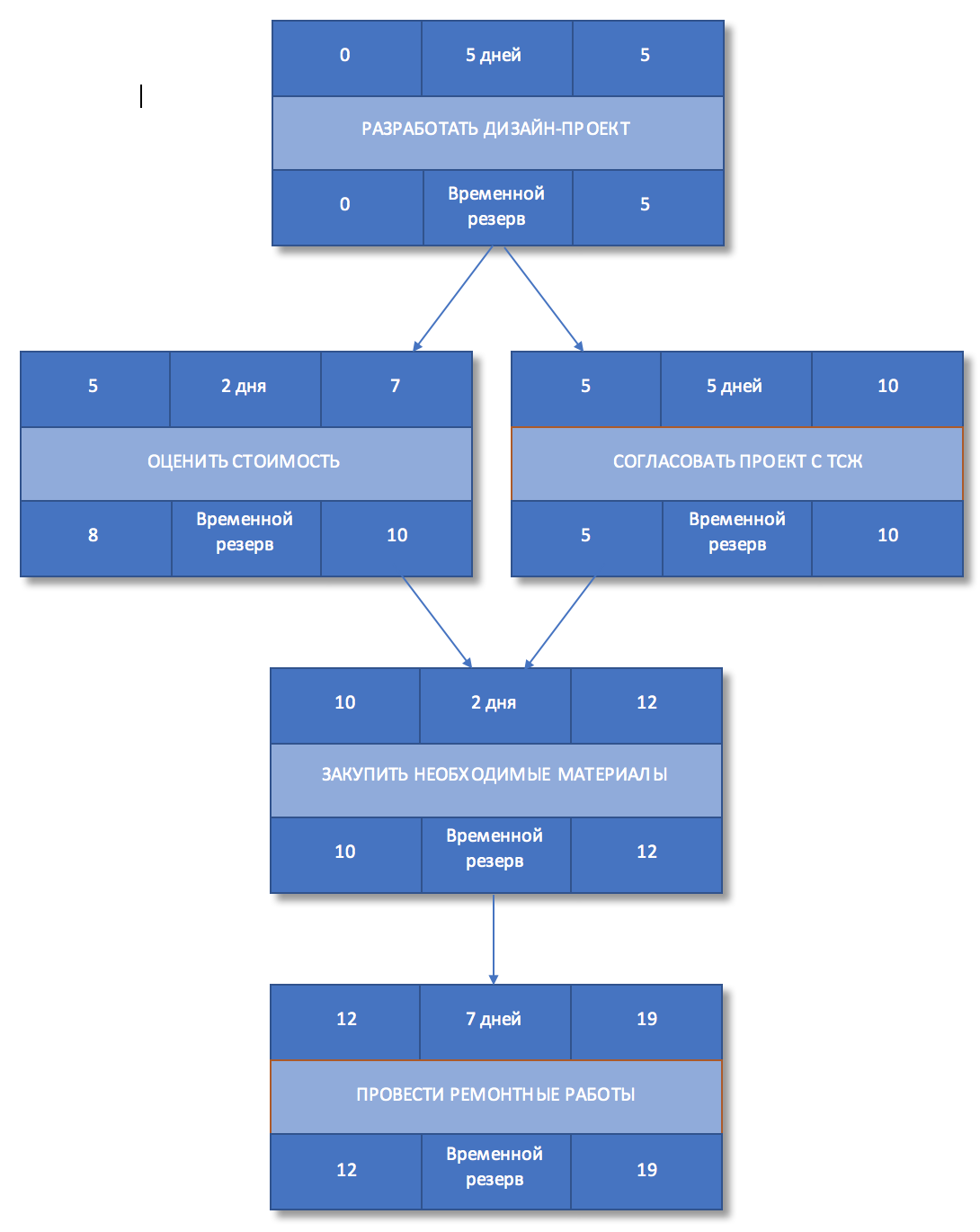
Рисунок 6. Позднее начало и окончание работ
Шаг 9. Определить временной резерв
Вычислим временной резерв для каждой из работ. Он вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
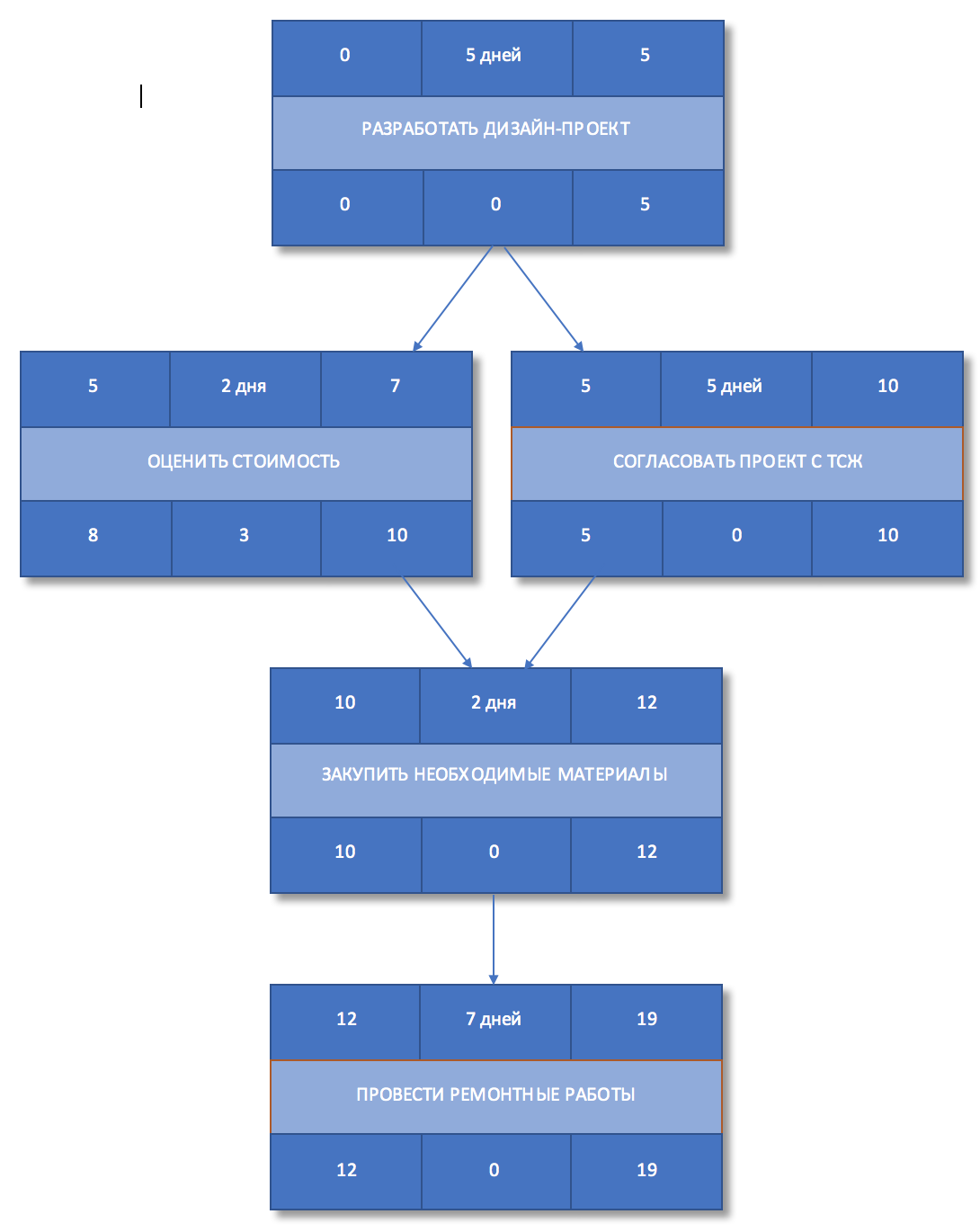
Рисунок 7. Временной резерв
Шаг 10. Выявить критический путь
Как мы уже знаем, критический путь — это цепочка работ, у которых резерв времени равен нулю. Выделим такие задачи на сетевом графике.

Рисунок 8. Критический путь
Задачи «Разработать дизайн-проект«, «Согласовать проект с ТСЖ» и «Закупить необходимые материалы«, «Провести ремонтные работы» составляю критический путь, а его длина составляет 19 дней. Это означает, что в текущем виде проект не может быть выполнен быстрее, чем за 19 дней. Если мы хотим сократить сроки проекта, то нам необходимо оптимизировать задачи, лежащие на критическом пути.
Например, мы можем начать ремонтные работы раньше получения согласования на перепланировку от ТСЖ, приняв на себя риски того, что согласование может быть не получено.
Просмотры:
47 538
Источник
Процесс расчета параметров сетевого графика
Сетевой график проекта располагает операции в подходящей последовательности для расчета времени начала и окончания операции. Оценка продолжительности операции проводится на основе затрат времени, требуемого для решения всех задач, составляющих набор работ операции.
С помощью нескольких простых расчетов можно выполнить прямой и обратный анализ сетевого графика проекта. Этот анализ даст ответы на следующие вопросы:
Прямой анализ – Определение ранних сроков начала операций
- Как скоро может начаться операция? (ранний старт – ES )
- Как скоро она может закончиться? (ранний финиш- EF )
- Как скоро может быть завершен проект в целом? (предполагаемое время- ТЕ )
Обратный анализ – Определение поздних сроков завершения операций
- Каковы самые поздние сроки начала операции? (позднее начало – LS )
- Каковы самые поздние сроки завершения операции? (позднее окончание – LF )
- Какие операции составляют критический путь ( СР )? Это самый длинный путь, при задержке выполнения операций на этом пути задерживается выполнение проекта.
- На какое время может быть задержано выполнение операции? (резерв времени – SL )
Термины в скобках являются общепринятыми обозначениями и используются в большинстве книг по управлению проектами
Прямой анализ – определение ранних сроков начала операций
Процесс прямого анализа разворачивается от первых операций проекта, проходя по всем цепочкам последовательных операций сетевого графика до самой последней операции проекта.
По мере продвижения по любому из путей производится добавление времени выполнения операций. Самый длинный путь показывает время завершения проекта в целом и называется критическим путем ( СР ).
В табл. 2.2 представлено время операций в рабочих днях для проекта бизнес-центра Колла.
На рис. 2.5 показана система с оценкой продолжительности операций, которую вы можете видеть в блоке.
Например, операция А имеет продолжительность 5 дней, операция G -170 рабочих дней.
Поступательный путь начинается со времени начала проекта, которое обычно принимается равным нулю.
Рис.
2.5.
Сетевой график типа ОУ для проекта создания бизнес-центра Колла
| Бизнес-центр Колла | |||
|---|---|---|---|
| Операция | Описание | Предшествующая операция | Время операции |
| А | Утверждение приложения | нет | 5 |
| В | Планы конструирования | А | 15 |
| С | Изучение трафика | А | 10 |
| D | Проверка наличия службы | А | 5 |
| Е | Отчет персонала | В, С | 15 |
| F | Одобрение комиссии | В, C, D | 10 |
| G | Ожидание работ | F | 170 |
| Н | Включение в работу | Е, G | 35 |
В нашем примере, ранний срок начала первой операции (операция- А ) это 0. Это время проставляется в верхнем левом углу блока операции А (рис. 2.6).
Самое раннее окончание операции А это 5 ( ES + Dur или 0 + 5 = 5 ).
Далее мы видим, что операция А предшествует операциям B, C, D.
Следовательно, самое раннее время начала этих операций – это момент завершения операции А, 5 рабочих дней.
На рис. 2.6 можно видеть, что операции В, С и D могут начаться в момент завершения операции А, и поэтому все они имеют раннее начало ( ES ) 5.
Используя формулу ES + Dur = EF, раннее время завершения этих операций – В, C, D -( EF ) будет, соответственно, 20, 15, и 10.
Рис.
2.6.
Прямой анализ сетевого графика для проекта создания бизнес-центра
Какое же тогда будет раннее время начала ( ES ) для операции Е, которая является операцией слияния?
Это будет 15 или 20? Ответ – 20, так как все операции, непосредственно предшествующие операции Е ( В и С ) должны быть завершены до начала операции Е. Поскольку для завершения операции В требуется более продолжительное время, она и определяет раннее начало ( ES ) операции Е.
Тот же процесс используется для определения ES для операции F. Ей предшествуют операции В, C, и D. Операция В является определяющей для времени раннего окончания ( EF ), которой требуется больше времени ( 20 против 15 и 10 ), чем операциям ( В, C, и D ), непосредственно предшествующим операции F.
Прямой анализ предполагает, что каждая операция начинается в тот момент, когда завершается последняя предшествующая ей операция. При расчете времени раннего начала операций в процессе прямого анализа необходимо помнить три вещи:
- Вы добавляете время операции на каждом шаге анализа ( ES + Dur = EF )
- Вы переносите раннее завершение ( EF ) предшествующей операции до следующей, у которой оно же становится временем раннего начала ( ES ), если только
- Последующая операция не является операцией слияния.В этом случае вы выбираете самое большое по значению время раннего окончания ( ЕF ) среди всех непосредственно предшествующих операций.
В нашем примере на рис. 2.6 ЕF для операции F (30) проводится до операции G, где становится ее ES (30).
Мы видим, что операция Н является операцией слияния и, следовательно, необходимо найти самое большое по значению EF у непосредственно предшествующих ей операций ( Е и G ). В этом случае выбор происходит между временем EF 35 и 200 ; выбор ES операции Н 200 EF для операции Н ( 235 ) становится самым ранним расчетным временем ( ТЕ ), когда проект может быть завершен в целом.
Таким образом, на все три вопроса, которые ставятся в процессе прямого анализа, были получены ответы.
Обратный анализ – определение поздних сроков завершения операций
Обратный анализ начинается с самой последней операции сетевого графика.
Каждый раз, выполняя шаг назад к началу сетевого графика, необходимо вычитать время рассматриваемой операции из общей продолжительности проекта в целом, с тем, чтобы определить сроки ее самого позднего возможного начала ( LS ) и окончания ( LF ) выполнения. За исходную временную точку при выполнении обратного анализа выбирается время позднего окончания самой последней операции проекта. В этой операции данное время совпадает с временем раннего окончания ее выполнения ( EF ) (или в случае нескольких завершающих операций, операции с самым большим ( EF )). В некоторых случаях имеются установленные крайние сроки продолжительности проекта, тогда будут использоваться именно эти сроки. Предположим, что мы можем принять EF предполагаемого окончания проекта ( ТЕ ) равным 235 рабочим дням. LF для операции Н становится 235 рабочих дней ( EF ~ LF ) (см. рис. 2.7).
Рис.
2.7.
Обратный анализ сетевого графика для проекта создания бизнес-центра
Обратный анализ похож на прямой. Выполняя его, следует помнить три вещи:
- Вы вычитаете время операции на каждом шаге, начиная с последней операции проекта ( LF – Dur = LS ).
- Вы переносите LS на предшествующую операцию и приравниваете ей LF к ней, если
- Предшествующая операция не является операцией дробления; в противном случае вы выбираете наименьший LS из всех операций, которым данная операция дает начало, и приравниваете к этому значению ее LF.
Давайте применим эти правила к нашему примеру с бизнес-центром Колла. Начинаем с операции Н (включение в работу) и ее LF в 235 рабочих дней, LS для операции Н оказывается равным 200 рабочих дней ( LF – Dur = LS или 235 – 35 = 200 ).
LS для операции Н становится LF для операций Е и G. LS для операций Е и G становится соответственно 185 ( 200 – 15 = 185 ) и 30 рабочих дней ( 200 – 170 = 30 ).
LS для операции G становится LF для операции F, и ее LS становится 20.
Здесь мы видим, что операции В и C являются операциями дробления, которые связаны с операциями Е и F. Поздний финиш для операции В контролируется LS операций Е и F. LS для операции Е – 185 дней и для операции F – 20 дней. Идите по стрелке назад от операций Е и F к операции В.
Отметим, что время LS для операций Е и F помещено в правый блок, и вы можете выбрать наименьшее время – 20 дней.
Заключительная операция В может быть завершена за 20 дней; в противном случае выполнение операции F задержится, задержится и выполнение проекта.
LF для операции C идентично операции В, поскольку она также определяет LS операций Е и F.
Операция D просто получает свое позднее окончание ( LF ) от операции F.
Вычислив LS ( LF – Dur = LS ) для операций В, C, D, мы можем определить LF для операции А, которая является операцией дробления.
Окончание операции А определяется операцией В, которая является наименьшим LS для операций В, С и D.
Так как LS для операции В составляет период времени 5, LF для операции А – 5, и ее LS – период времени – 0.
Обратный анализ завершен, и сроки последней операции известны.
Источник
Аннотация: От набора работ к сетевому графику. Конструирование сетевого графика проекта, два подхода к разработке сетевых графиков. Основные правила разработки сетевого графика. Принципы построения и анализа сетевых графиков типа “ОУ”. Оценка начала и окончания работ с помощью сетевого графика. Процесс расчета параметров сетевого графика. Прямой анализ – определение ранних сроков начала операций. Обратный анализ — определение поздних сроков завершения операций. Использование результатов прямого и обратного анализа сетевого графика. Ошибки сетевой логики. Приближение к реальности посредством улучшенных методов построения сетевых графиков. Использование задержек (лагов). Отношения типа “от конца к началу”. Отношения “от начала к началу”. Отношения “от конца к концу”. Отношения “от начала к концу”. Комбинация отношений задержки. Операции растяжки
Сетевой график отражает операции проекта, которые необходимо выполнить, логическую последовательность и взаимозависимость этих операций и время начала и окончания самой продолжительной цепочки операций – критический путь.
Сетевой график раскрывает внутренние связи проекта и служит основой для календарного планирования работ и использования оборудования.
Сетевой график дает возможность оценить периоды времени, в течение которых выполнение операций может начинаться и заканчиваться, а также время допустимой задержки их выполнения.
Сетевой график позволяет определить, какие операции являются “критическими” и, следовательно, должны выполняться строго по графику, чтобы проект был завершен в запланированные сроки.
От набора работ к сетевому графику
Сетевой график строится при помощи прямоугольников (блоков) и стрелок.
На рис. 2.1 блок обозначает операцию и стрелка показывает подчиненность операций и направленность хода выполнения проекта.
Рис.
2.1.
Развертка сетевых графиков
Операция представляет одну или несколько задач, требующих определенных затрат времени.
Наборы работ используются для разработки детального сетевого графика для руководителей первого уровня (см. уровень 3 “Планы” на рис. 2.1).
Подробные графики двух проектов для руководителей отделов (уровень 2) могут быть объединены в более агрегированную форму и, далее, могут быть сведены к самому общему виду, необходимому для руководителя проекта, высшего руководства и клиента.
Этот верхний уровень обычно представлен в виде графика Ганта и называется планом контрольных точек.Достоверность информации на каждом уровне зависит от точности определения набора работ и операций.
Первое, что нужно сделать для разработки сетевого графика проекта, определить набор работ.
Рис. 2.2 показывает часть структурированного набора работ и как информация используется для разработки сетевого графика.
Рис.
2.2.
Перевод наборов работ в сетевой график
Самый нижний уровень набора работ, подлежащих выполнению на рис. 2.2, называется условно “Печатная плата”.
Счета издержек (на дизайн, на производство, на испытания, на разработку программного обеспечения) обозначают соответствующую проектную работу, отвечающий за нее отдел и бюджет времени, отведенный для ее выполнения. Каждый счет издержек представляет один или несколько наборов работ.
Рис. 2.2 показывает, как наборы работ используются для разработки сетевого графика проекта. Использование наборов работ можно отследить при помощи специальной системы кодирования. Например, в операции А используется рабочий пакет D-1-1 и D-1-2 (спецификация и документация), тогда как операция C использует рабочий пакет S-22-1. Управляющий проектом дает оценку времени выполнения всей операции, исходя из времени на выполнение отдельных работ в наборе. Например, выполнение операции В (прототип 1) потребует 5 недель; операции К (тестирование) -3 недели. После расчета начала и окончания выполнения операций менеджер может определить необходимые ресурсы и составить поэтапный бюджет проекта (с датами).
Конструирование сетевого графика проекта
Терминология
Операция (или работа). Для руководителей проектов операция – это неделимый элемент проекта, требующий затрат времени для своего выполнения.
Обычно выполнение операций связано с затратами времени и трудовых ресурсов.
Иногда это может быть просто время. Примерами этого могут быть операция ожидания подписания контракта или ожидание поступления материалов, одобрения правительства, таможенное оформление грузов и т.д.
Операции обычно состоят из одной или более работ из наборов работ. Как правило, название операциям дается в повелительной форме глагола, например, “разработать спецификацию продукта”.
Операция слияния.Это операция, которая имеет более одной непосредственно предшествующей ей операции.
Параллельные операции.Это операции, которые могут, по желанию менеджера, выполняться одновременно. Однако совсем не обязательно осуществлять параллельные операции одновременно.
Путь.Последовательность связанных, взаимозависимых операций.
Критический путь.Это самый длинный путь во всей системе операций; если выполнение операции на этом отрезке задерживается, выполнение всего проекта задерживается на такое же время.
Событие.Термин используется для обозначения точки времени начала или завершения операции. Событие не требует времени.
Дробящаяся операция.Это операция, за которой сразу следуют несколько операций (от нее исходит более одной стрелки, обозначающей зависимость).
Два подхода к разработке сетевых графиков
Для разработки сетевых графиков могут применяться два подхода:
подход с обозначением операций в узлах (блоках) графика – ОУ ;
подход с обозначением операций на стрелках графика – ОС.
На практике первый метод – ОУ – используется значительно чаще и далее излагается именно этот метод.
Основные правила разработки сетевого графика
При разработке сетевого графика целесообразно придерживаться следующих 8 правил:
- Сетевой график разворачивается слева направо.
- Ни одна операция не может быть начата, пока все предшествующие связанные с ней операции не будут выполнены.
- Стрелки в сетевом графике отображают отношения предшествования и следования. На рисунке стрелки могут пересекаться.
- Каждая операция должна иметь свой собственный номер.
- Номер последующей операции должен быть больше номера любой предшествующей операции.
- Образование петель недопустимо (другими словами, не должно происходить зацикливания хода выполнения установленного набора операций).
- Условные переходы от одной операции к другой не допускаются (имеется в виду определение последовательности хода выполнения операций условиями типа: “Если будет достигнут успех, сделайте то-то…; если нет – ничего не предпринимайте”).
- Опыт показывает, что когда существует несколько исходных операций проекта, то может быть определен общий узел начала всего комплекса работ. Точно так же один узел может быть использован для четкого обозначения окончания проекта.
Источник
